Application Note 装置とアッセイ比較に最適な評価指標
PDF版(英語)
はじめに
装置を比較する際には、その性能を測定するための指標(メトリクス)を選択する必要があります。一般的には、装置の「感度」に関心がありますが、感度はさまざまな方法で測定できます。感度評価に用いられる指標には、シグナル対バックグラウンド比(S/B)、シグナル対ノイズ比(S/N)、検出下限(LLD)、およびZ’-factorがあります *1。
基本的には、あるアッセイに対して装置がシグナルを検出できるかどうか、つまり装置のバックグラウンドを超えてシグナルが検出可能かどうかが重要です。シグナルをバックグラウンドより上で検出できるかどうかは、平均シグナルや平均バックグラウンドレベルだけでなく、シグナルやバックグラウンドの変動といった他の要因にも依存します。
これを理解するために、群衆の中で身長1.9 mの友人を探すという例えを考えてみましょう:
- 群衆の他の人が全員1.6 mなら、平均バックグラウンドは均一でシグナル(友人)より低いため、友人は明確に見えます。
- 群衆の他の人が全員1.9 mなら、シグナルは平均バックグラウンドと同じです。バックグラウンドノイズは低いものの、平均バックグラウンドが高いため友人は見えません。
- 最後に、群衆の身長が1.5~2 mの範囲で均等に分布している場合、平均バックグラウンドは1.75 mです。平均バックグラウンドはシグナルより低いですが、身長のばらつき(ノイズ)が大きいため、友人を見つけるのは難しくなります。
したがって、検出限界を決定する際には、シグナル、平均バックグラウンド、バックグラウンドの変動をすべて考慮する必要があります。
さらに、この例えを友人の集団(ポピュレーション)に拡張すると、シグナルの変動も重要になります(全員が同じ身長なら見つけやすく、身長が異なる場合でも群衆より高ければ見つけやすい)。
このように、装置比較のためのメトリクスを評価する際に重要なパラメータは以下の通りです:
- 平均シグナル
- シグナル変動
- 平均バックグラウンド
- バックグラウンドの変動
シグナル対バックグラウンド比
シグナル対バックグラウンド比は、平均シグナルレベルと平均バックグラウンドレベルの比率です:
$$ S / B = \frac{\text{mean signal}}{\text{mean background}} $$
前述のとおり、シグナル対バックグラウンド比は感度の指標として不十分です。なぜなら、シグナルの変動やバックグラウンドの変動に関する情報を含んでいないからです *2(図1および図2参照)。シグナル対バックグラウンド比では、平均バックグラウンドが同じであっても、バックグラウンドの変動が大きい装置と小さい装置を区別することができません。
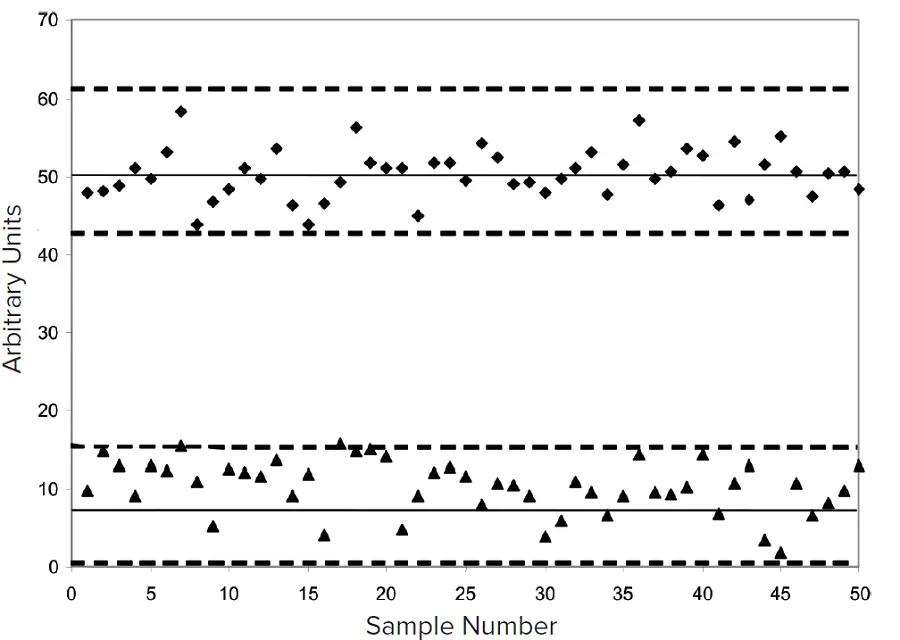
図1. シグナルとバックグラウンド(バックグラウンド変動が大きい場合)
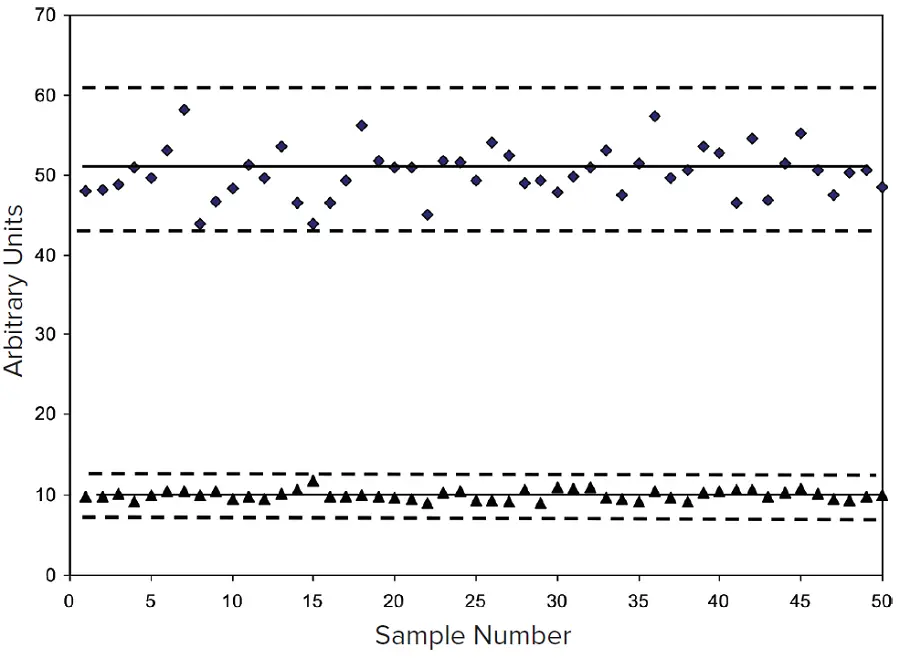
図2. シグナルとバックグラウンド(バックグラウンド変動が小さい場合)
シグナル対ノイズ比
シグナル対ノイズ比は、バックグラウンドの変動を考慮するため、シグナル対バックグラウンド比よりも優れた指標です:
$$ S / N = \frac{\text{mean signal - mean background}}{\text{standard deviation of background}} $$
シグナル対ノイズ比は、特定の値のシグナル、特にバックグラウンド付近のシグナルをどの程度の確信をもって定量できるかを判断するための重要で広く使用される指標です。バックグラウンドシグナルの変動(「ノイズ」)が小さいほど、平均バックグラウンドの絶対値に関係なく、シグナルの定量に対する信頼性は高まります。
図1と図2のデータは同じシグナル対バックグラウンド比を示していますが、バックグラウンドの変動が小さいため、図2のシグナル対ノイズ比は図1よりも高くなっています。
ただし、シグナル対ノイズ比はシグナルの変動を考慮しないため、バックグラウンドの変動が同じでもシグナルの変動が異なる装置を区別することはできません。
検出下限(Limit of Detection)
検出下限は、シグナル対ノイズ比と同様にバックグラウンドの変動を考慮するため、装置比較に適した指標です:
$$ \text{LLD} = \frac{3 \times \text{standard deviation of background}} {\dfrac{\text{mean sample} - \text{mean background}}{\text{sample concentration}}} $$
バックグラウンドの変動が大きくなると、検出下限も増加します。また、シグナル対ノイズ比と同様に、シグナルの変動は考慮されません。
Z'-factor
Z’-factorは、ハイスループットスクリーニング分野で、試験化合物に依存しないスクリーニングアッセイの品質を測定するための標準的な統計パラメータです。これは、アッセイにおけるポジティブコントロールとネガティブコントロール間のシグナル分離を評価する指標として使用され、装置性能の測定と比較に有用な4つのパラメータすべてを含んでいます。
Z’-factorは次の式で計算されます:
$$ Z' = 1 - \frac{3\sigma_{c+} + 3\sigma_{c-}}{|\mu_{c+} \text{ and } \mu_{c-}|} $$
ここで、σc+ と σc– はそれぞれポジティブコントロール群とネガティブコントロール群の標準偏差を示し、μc+ と μc– はポジティブコントロール群とネガティブコントロール群の平均値を示します。
Z’は線形ではなく、いずれかの集団で標準偏差を歪める外れ値によって、非現実的に小さな値になる可能性があります。
Z’値の分布と解釈:
- 約1 = 完全なアッセイ
- 0.5 = ポジティブコントロールとネガティブコントロールの差の約半分に相当する明確なウィンドウ
- 0.4 = 一般的にアッセイの許容最小値
- 0 = ポジティブコントロールとネガティブコントロールの集団が3σレベルで重なります
- <0 = 大きな重なり
Z’の重要性は、図3のようにグラフィカルに表すとさらに理解しやすくなります。
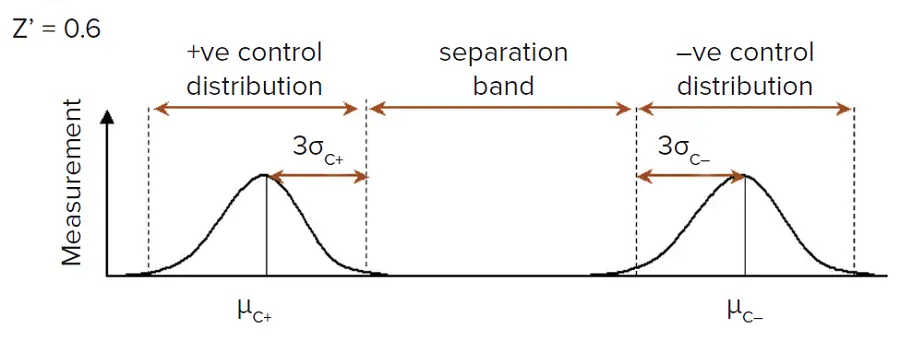
図3. Z’-factorによるポジティブコントロールとネガティブコントロールの分離 *3。
シグナル対ノイズ比や検出下限とは異なり、Z’-factorはシグナルの変動を考慮します。したがって、これら2つの指標とは異なり、シグナルの変動に基づいて装置を区別することができます。
図4は、2つのプレートリーダーAとBから得られたデータの例を示しています。直感的には、バックグラウンドの変動が大きいものの、シグナルの変動が小さく、シグナルとバックグラウンドのデータ間に明確な分離があるため、リーダーAのデータを好ましく感じます。対照的に、リーダーBはバックグラウンドの変動が小さいものの、シグナルの変動が非常に大きいです。この違いは各指標の値に反映されます。Z’はシグナルの変動を含むため、リーダーAはZ’でリーダーBより高いスコアを示しますが、シグナル対ノイズ比やシグナル対バックグラウンド比ではリーダーBの方が高いスコアを示します。
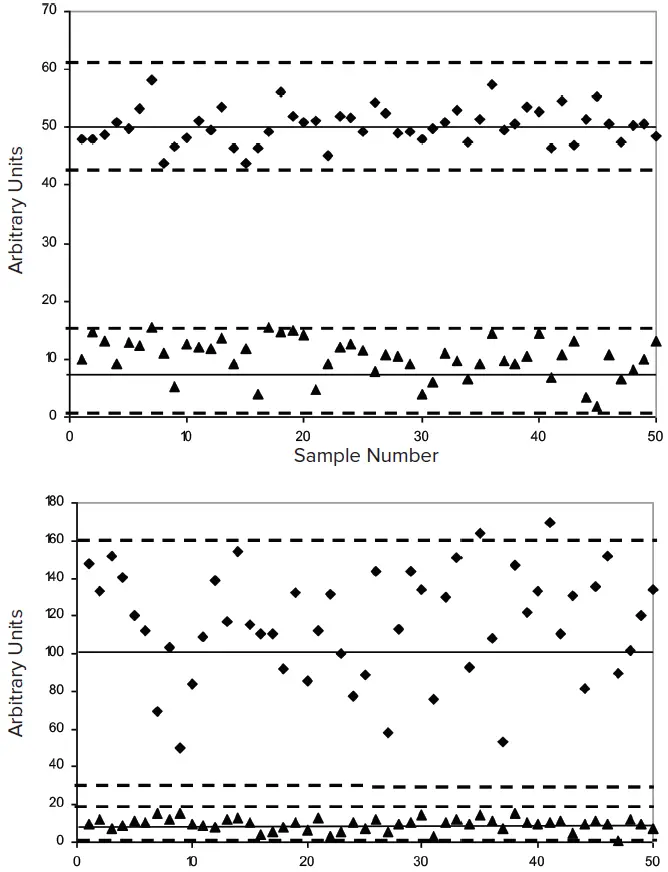
図4. Z’-factorの例 *4 上段:S/B = 5、S/N = 12、Z’ = 0.5 下段:S/B = 12、S/N = 32、Z’ = 0.1
参考文献
- Zhang JH, Chung TD, Oldenburg KR, “A Simple Statistical Parameter for Use in Evaluation and Validation of High Throughput Screening Assays.” J Biomol Screen. 1999;4(2):67–73.
- Zhang et al., ibid., “Because the S/B ratio does not contain any information regarding data variation, its inappropriateness in evaluation of an assay should be obvious.”
- Following Figure 4 in Zhang et al., ibid.
- Following Figure 1 in Zhang et al., ibid.
PDF版(英語)